Seven Ways to Groove in 11/8

Not surprisingly, a pulse of eleven eighth- or quarter-notes per measure offers a lot of potential for rhythmic subdivisions. 

In this lesson, we’re checking out seven ways to groove in 11/8, and applying each one to some real-life situations. (Keep in mind that all of the following examples can be adapted to 11/4 by halving the tempo and doubling the value of each note.)

First up are the obvious lopsided 6 +5 and 5 + 6 divisions (Examples 1a and 1b). Work on one at a time by establishing a tempo within the suggested range and tapping your foot to the notated accents while observing how you have to double up foot taps (i.e. two eighth-note taps in a row) when going from odd to even subgroupings. Find the groove, add some single notes or chords, and you’re off and running.

Ex. 1c features a loping, triplet-based 3 + 3 + 3 + 2 subdivision that easily translates to the 11/8 shuffle beat shown in Ex. 1d. Note the changes in the accented foot taps. (Tip: Try mixing and matching the previous four examples to practice transitioning between the various groupings.) 

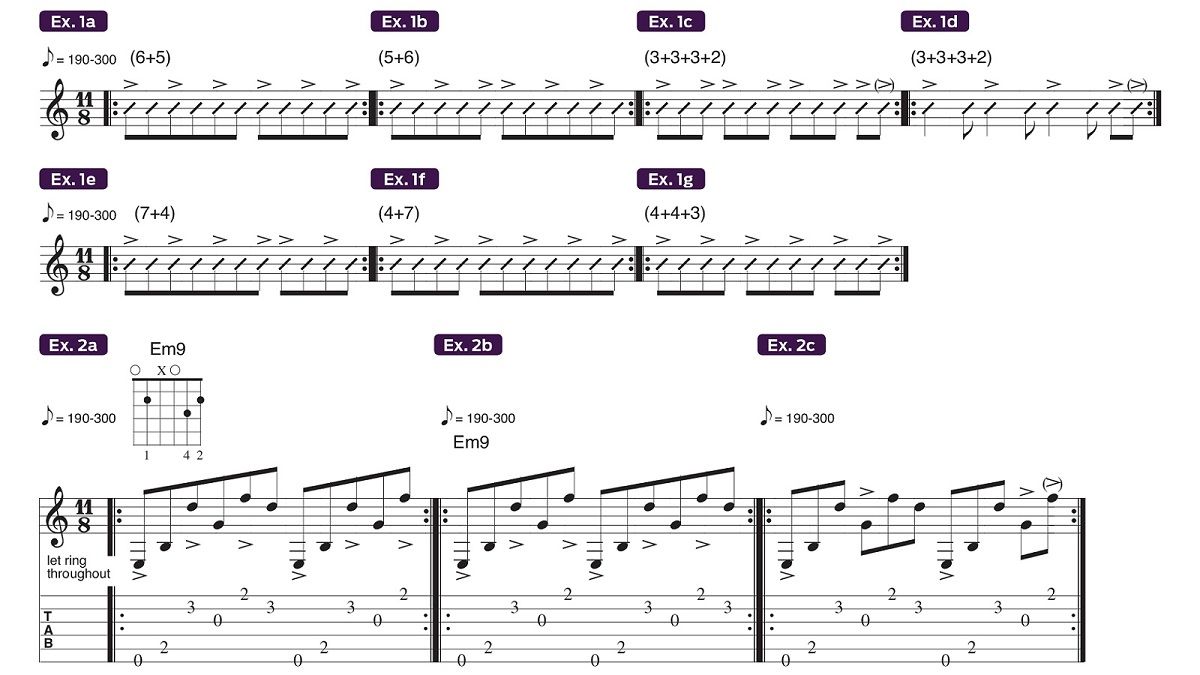
Examples 1e and 1f focus on 7 + 4 and 4 + 7 divisions respectively, where again, you’ll encounter two eighth-note foot taps in a row when crossing from odd to even groups. Finally, Ex. 1g details a 4 + 4 + 3 (or 8 + 3) subdivision, which is essentially the same as Ex. 1f’s 4 + 7 grouping. Let’s send them all into action.

The next three examples feature a single chord shape (Em9) arpeggiated in accordance with Examples 1a through 1c. 

Choose a picking technique - pick only, fingerstyle or hybrid pick-and-fingerstyle (or better yet, all three) - and have at the 6 + 5 grouping in Ex. 2a, the 5+6 grouping in Ex. 2b and the 3 + 3 + 3 + 2 subdivision in Ex. 2c. Though all three are similar, it’s the different sets of accents that make each one unique.

Shifting to a single-note figure, Ex. 3a transforms the subdivision from Ex. 1c into a propulsive, E-based blues/rock riff. 

Ex. 3b applies the elongated, shuffle version of the same division (from Ex. 1d) to a pair of alternating E5 and E6 chords for an 11/8 shuffle that wouldn’t sound out of place in a Mahavishnu Orchestra jam. 

Ex. 3c makes use of Ex. 1g’s 4 + 4 + 3 grouping with a single-note, E-Mixolydian-based ’70s-fusion riff that doubles the value of the first, third, fifth and seventh eighth-notes to form a four-quarter-note plus three-eighth-note motif.

Ex. 4a portrays another E Mixolydian riff grafted to the 7 + 4 division from Ex. 1e, but just in case you’re getting the idea that 11/8 meter is exclusive to jazz or fusion, play Ex. 4b’s 3 + 3 + 3 + 2 subdivision circa 198 bpm, which suggests perhaps the most famous 11/8 figure in blues-rock history - the intro to the Allman Brothers Band’s “Whipping Post.”

As with any odd time signature, sixteenth-note subdivisions open up a whole new can of worms. Ex. 5a is related to the 3 + 3 + 3 + 2 grouping from Ex. 1c, but here the first nine eighth-notes are further subdivided into six dotted-eighths, which creates a 3/16, three-against-two hemiola that recycles via the last two eighth-notes in the measure. 

The description sounds complicated, but the actual rhythm flows very naturally. Ex. 5b further clarifies the 3/16 groupings and is more applicable to single notes than chords. (Tip: Tap your foot on the accents.)

Ex. 6a shows what happens when the divisions from Ex. 5a are applied to melodic motion below static pedal tones to create D, Bb and Gm harmonies. 

The repetitive three-bar figure - reminiscent of the Jan Hammer Group’s “Magical Dog,” from Oh, Yeah!, a virtual treasure trove of odd time signatures - is a very flowing figure that can easily make you forget it’s in 11/8, a goal worth striving for. 

Finally, Ex. 6b transforms the previous partial D-chord shape into a non-stop sixteenth- note run, where each melody note is followed by a pair of pedal tones - A, the 5 - for the first nine eighth-notes, and then a single pedal between beats 10 and 11. Apply the same architecture to the partial Bb and Gm shapes from Ex. 6a to complete the three-bar cycle and blast off!